Polynomial Regressions
To find the regression equation for a polynomial, you must create a system of equations. To solve these systems of equations it is easiest to express them as matrices.
Below is the general formula to creating matrices to solve a polynomial regression.
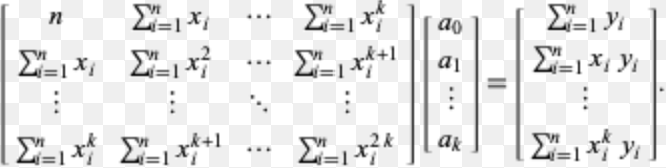
In the above picture, each ak represents one of the coefficients in your regression. So, if you were making a quadratic regression, you would need to find a0, a1, and a2.
Below is the equation you could set up to find a quartic regression.
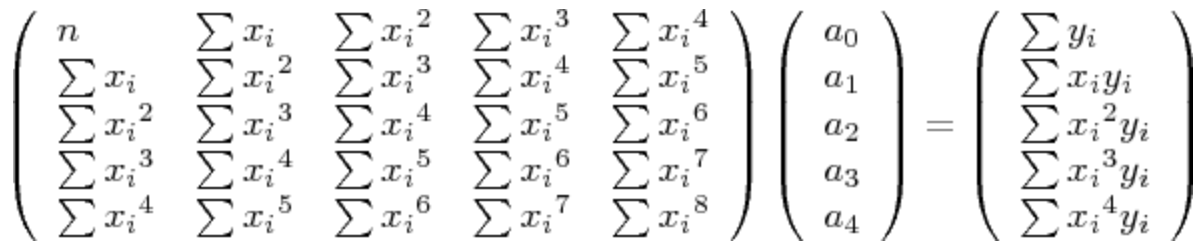
Yes, it's as painful as it looks.
Integrating the Normal Curve
To find the probability in hypothesis tests, the area of the normal curve from either -Infinity or +Infinity to some z-score is needed. Unfortunately, integrating the normal curve is no easy task.
Below is the equation for the normal curve.
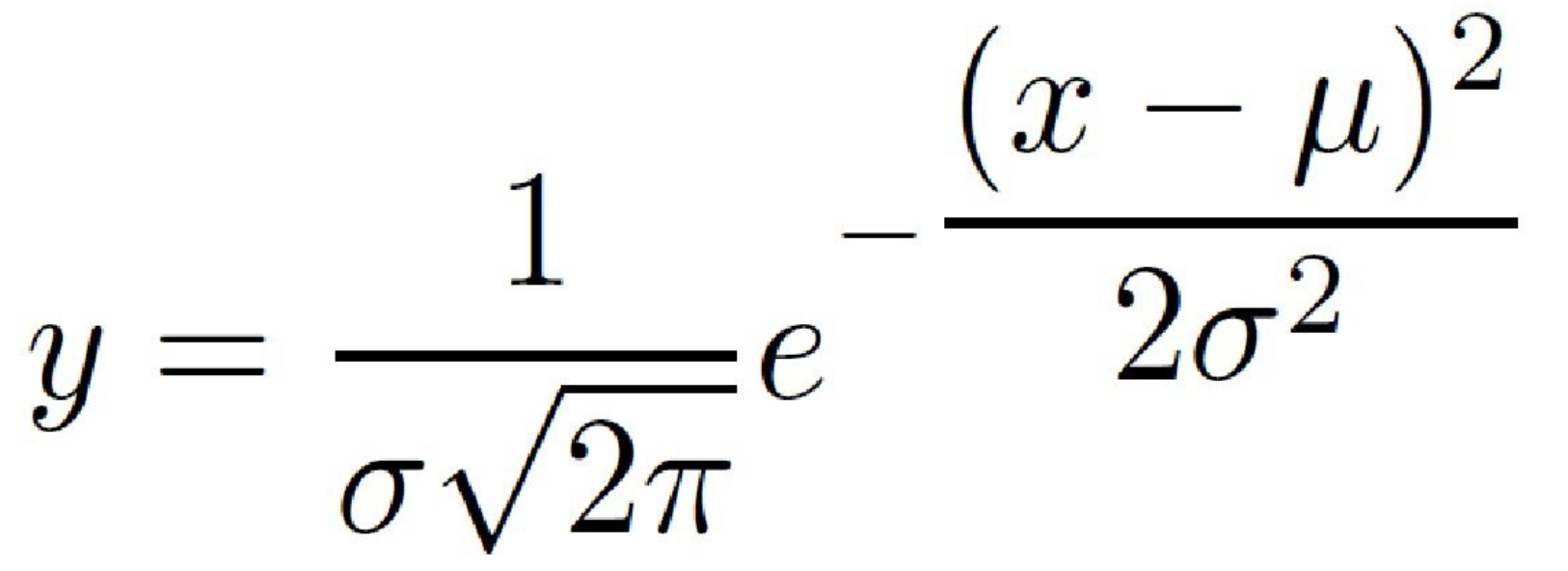
For the rest of this explanation, I'll be assuming our normal curve has a mean of 0 and a standard deviation of 1, though this process will work with other values.
Here is the setup to find the area under the normal curve from 0 to some z-score.
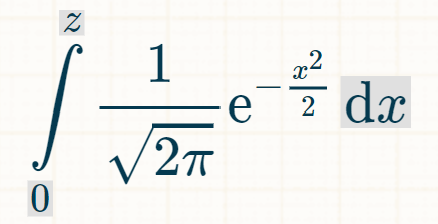
This cannot be integrated algebraically. Instead, we can use something called the Gauss error function (erf).
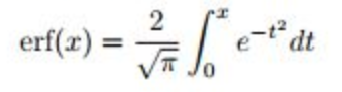
In order to use this error function, we need to employ some u substitution.
u = x / √(2)
u = x / √(2) --> du/dx = 1 / √(2) --> dx = √(2)du
Now we can rewrite our integral like this:
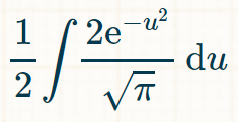
Which is the same as...
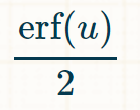
Now substitute x / √(2) for u...
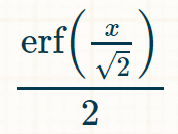
But what is the error function? The error function cannot be expressed algebraically, but one way that it can be expressed is with a Taylor series. The Taylor series of the error function is a manipulation of the Taylor series for ex.
This is the maclaurin series for the error function:
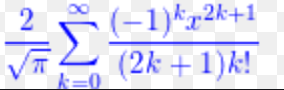
This application uses a 21st degree Maclaurin polynomial to approximate the probability during a hypothesis test. Unfortunately, because only the maclaurin series is used to approximate the area, hypothesis tests with |z-scores| greater than 3 will get inaccurate probabilities.